When using the Loco Positioning System the Kalman estimator is used for position estimation. The two main ranging schemes used for UWB localization are (i) two-way ranging (TWR) and (ii) time-difference-of-arrival (TDoA). In this page, we elaborate the measurement model, Kalman filter update and robust estimation for both TWR and TDoA.
Two-way ranging (TWR)
In TWR, the UWB tag mounted on the Crazyflie communicates with fixed UWB anchors and acquires range measurements through two-way communication. The measurement model is as follows:
,
where is the position of the Crazyflie and is the position of the fixed anchor i. For the conventional extended Kalman filter, we have
.
The H vector is
.
Then, we call the function kalmanCoreScalarUpdate() in kalman_core.c to update the states and covariance matrix.
Time-difference-of-arrival (TDoA)
In TDoA, UWB tags receive signals from anchors passively and compute the difference in distance beween two anchors as TDoA measurements. Since in TDoA scheme, UWB tags only listen to the messages from anchors, a TDoA-based localization system allows a theoretically unlimited number of robots to localize themselves with a small number of fixed anchors. However, TDoA measurements are more noisy than TWR measurements, leading to a less accurate localization performance. Two types of TDoA protocols (TDoA2 and TDoA3) are implemented in LPS system. The main difference between the two TDoA protocols is that TDoA3 protocol achieves the scalability at the cost of localization accuracy. The readers are refer to TDoA2 VS TDoA3 for detailed information.
The TDoA measurement model is as follows:
,
where is the position of the Crazyflie and and are the positions of fixed anchor i and j, respectively. For the conventional extended Kalman filter, we have
.
The H vector is
.
Then, we call the function kalmanCoreScalarUpdate() in kalman_core.c to update the states and covariance matrix.
M-estimation based robust Kalman filter
UWB radio signal suffers from outlier measurements caused by radio multi-path reflection and non-line-of-sight propagation. The large erroneous measurements often deteriorate the accuracy of UWB localization. The conventional Kalman filter is sensitive to measurement outliers due to its intrinsic minimum mean-square-error (MMSE) criterion. Here, we provide a robust estiamtion approach based on M-estimation robust cost function. We will explain the general idea of the robust Kalman filter and readers are encouraged to look into the firmware mm_distance_robust.c and mm_tdoa_robust.c. The implementation is based on paper [1] and please read the paper for implementation details.
From the Bayesian maximum a posteriori perspective, the Kalman filter state estimation framework can be derived by solving the following minimization problem:
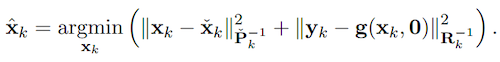
Therein, and are the system state and measurements at timestep k, and denote the prior covariance and measurement covariance, respectively. Through Cholesky factorization of and $$R_k$ $, the original optimization problem is equivalent to:
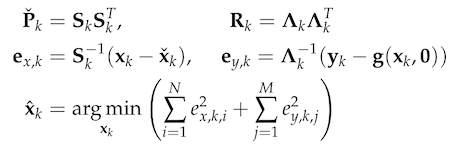
where and are the elements of and . To reduce the influence of outliers, we incorporate a robust cost function into the Kalman filter framework as follows:
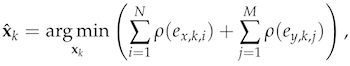
where could be any robust function (e.g., G-M, SC-DCS, Huber, Cauchy, etc.)
By introducing a weight function for the process and measurement uncertainties—with e as input—we can translate the optimization problem into an Iterative Reweight Least-Square (IRLS) problem. Then, the optimal posterior estimate can be computed through iteratively solving the least-square problem using the robust weights computed from the previous solution. In our implementation, we use the G-M robust cost function and the maximum iteration is set to be two for computational frugality. Then, we call the function kalmanCoreUpdateWithPKE() in kalman_core.c with the weighted covariance matrix , kalman gain Km, and innovation error to update the states and covariance matrix.
This functionality can be turned on through setting a parameter (kalman.robustTwr or kalman.robustTdoa).
References
[1] Zhao, Wenda, Jacopo Panerati, and Angela P. Schoellig. “Learning-based Bias Correction for Time Difference of Arrival Ultra-wideband Localization of Resource-constrained Mobile Robots.” IEEE Robotics and Automation Letters 6, no. 2 (2021): 3639-3646.