This week we have a guest blog post from Wenda Zhao, Ph.D. candidate at the Dynamic System Lab (with Prof. Angela Schoellig), University of Toronto Institute for Aerospace Studies (UTIAS). Enjoy!
Accurate indoor localization is a crucial enabling capability for indoor robotics. Small and computationally-constrained indoor mobile robots have led researchers to pursue localization methods leveraging low-power and lightweight sensors. Ultra-wideband (UWB) technology, in particular, has been shown to provide sub-meter accurate, high-frequency, obstacle-penetrating ranging measurements that are robust to radio-frequency interference, using tiny integrated circuits. UWB chips have already been included in the latest generations of smartphones (iPhone 12, Samsung Galaxy S21, etc.) with the expectation that they will support faster data transfer and accurate indoor positioning, even in cluttered environments.

In our lab, we show that a Crazyflie nano-quadcopter can stably fly through a cardboard tunnel with only an IMU and UWB tag, from Bitcraze’s Loco Positioning System (LPS), for state estimation. However, it is challenging to achieve a reliable localization performance as we show above. Many factors can reduce the accuracy and reliability of UWB localization, for either two-way ranging (TWR) or time-difference-of-arrival (TDOA) measurements. Non-line-of-sight (NLOS) and multi-path radio propagation can lead to erroneous, spurious measurements (so-called outliers). Even line-of-sight (LOS) UWB measurements exhibit error patterns (i.e., bias), which are typically caused by the UWB antenna’s radiation characteristics. In our recent work, we present an M-estimation-based robust Kalman filter to reduce the influence of outliers and achieve robust UWB localization. We contributed an implementation of the robust Kalman filter for both TWR and TDOA (PR #707 and #745) to Bitcraze’s crazyflie-firmware open-source project.
Methodology
The conventional Kalman filter, a primary sensor fusion mechanism, is sensitive to measurement outliers due to its minimum mean-square-error (MMSE) criterion. To achieve robust estimation, it is critical to properly handle measurement outliers. We implement a robust M-estimation method to address this problem. Instead of using a least-squares, maximum-likelihood cost function, we use a robust cost function to downweigh the influence of outlier measurements [1]. Compared to Random Sample Consensus (RANSAC) approaches, our method can handle sparse UWB measurements, which are often a challenge for RANSAC.
From the Bayesian maximum-a-posteriori perspective, the Kalman filter state estimation framework can be derived by solving the following minimization problem:
Therein, xk and yk are the system state and measurements at timestep k. Pk and Rk denote the prior covariance and measurement covariance, respectively. The prior and posteriori estimates are denoted as xk check and xk hat and the measurement function without noise is indicated as g(xk,0). Through Cholesky factorization of Pk and Rk, the original optimization problem is equivalent to
where ex,k,i and ey,k,j are the elements of ex,k and ey,k. To reduce the influence of outliers, we incorporate a robust cost function into the Kalman filter framework as follows:
where rho() could be any robust function (G-M, SC-DCS, Huber, Cauchy, etc.[2]).
By introducing a weight function for the process and measurement uncertainties—with e as input—we can translate the optimization problem into an Iteratively Reweighted Least Squares (IRLS) problem. Then, the optimal posteriori estimate can be computed through iteratively solving the least-squares problem using the robust weights computed from the previous solution. In our implementation, we use the G-M robust cost function and the maximum iteration is set to be two for computational reasons. For further details about the robust Kalman filter, readers are referred to our ICRA/RA-L paper and the onboard firmware (mm_tdoa_robust.c and mm_distance_robust.c).
Performance
We demonstrate the effectiveness of the robust Kalman filter on-board a Crazyflie 2.1. The Crazyflie is equipped with an IMU and an LPS UWB tag (in TDOA2 mode). With the conventional onboard extended Kalman filter, the drone is affected by measurement outliers and jumps around significantly while trying to hover. In contrast, with the robust Kalman filter, the drone shows a more reliable localization performance.
The robust Kalman filter implementations for UWB TWR and TDOA localization have been included in the crazyflie-firmware master branch as of March 2021 (2021.03 release). This functionality can be turned on by setting a parameter (robustTwr or robustTdoa) in estimator_kalman.c. We encourage LPS users to check out this new functionality.
As we mentioned above, off-the-shelf, low-cost UWB modules also exhibit distinctive and reproducible bias patterns. In our recent work, we devised experiments using the LPS UWB modules and showed that the systematic biases have a strong relationship with the pose of the tag and the anchors as they result from the UWB radio doughnut-shaped antenna pattern. A pre-trained neural network is used to approximate the systematic biases. By combining bias compensation with the robust Kalman filter, we obtain a lightweight, learning-enhanced localization framework that achieves accurate and reliable UWB indoor positioning. We show that our approach runs in real-time and in closed-loop on-board a Crazyflie nano-quadcopter yielding enhanced localization performance for autonomous trajectory tracking. The dataset for the systematic biases in UWB TDOA measurements is available on our Open-source Code & Dataset webpage. We are also currently working on a more comprehensive dataset with IMU, UWB, and optical flow measurements and again based on the Crazyflie platform. So stay tuned!
Reference
[1] L. Chang, K. Li, and B. Hu, “Huber’s M-estimation-based process uncertainty robust filter for integrated INS/GPS,” IEEE Sensors Journal, 2015, vol. 15, no. 6, pp. 3367–3374.
[2] K. MacTavish and T. D. Barfoot, “At all costs: A comparison of robust cost functions for camera correspondence outliers,” in IEEE Conference on Computer and Robot Vision (CRV). 2015, pp. 62–69.
Links
- Video: https://youtu.be/J32mrDN5ws4
- Paper: https://arxiv.org/abs/2103.01885
- Our Lab: http://www.dynsyslab.org
The authors are with the Dynamic Systems Lab, Institute for Aerospace Studies, University of Toronto, Canada, and affiliated with the Vector Institute for Artificial intelligence in Toronto.
Feel free to contact us if you have any questions or suggestions: wenda.zhao@robotics.utias.utoronto.ca.
Please cite this as:
<code>@ARTICLE{Zhao2021Learningbased,
author={W. {Zhao} and J. {Panerati} and A. P. {Schoellig}},
title={Learning-based Bias Correction for Time Difference of Arrival Ultra-wideband Localization of Resource-constrained Mobile Robots},
journal={IEEE Robotics and Automation Letters},
volume={6},
number={2},
pages={3639-3646},
year={2021},
publisher={IEEE}
doi={10.1109/LRA.2021.3064199}}
</code>
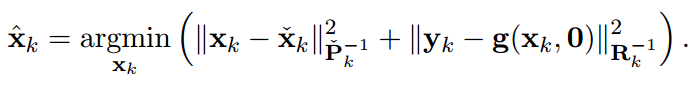
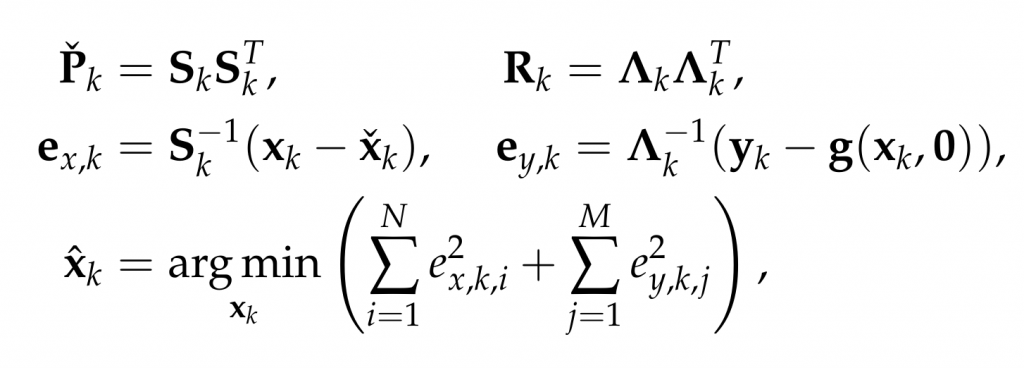
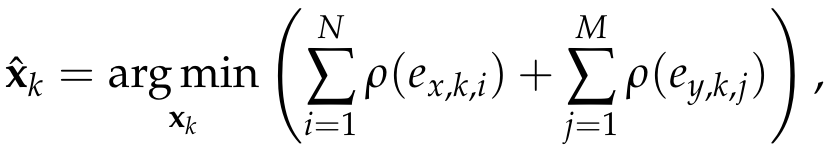


That’s interesting. We’ll try it!
Thanks!
hi,
uwb+imu, how about the accuracy ?
Hello,
The localization performance for UWB+IMU depends on many factors. Among them, UWB constellations, UWB biases, and environmental RF noises are the three major ones, especially for TDOA-based localization.
A quick answer to your question.
With an out-of-the-box Crazyflie 2.0 quadcopter and LPS bundle, the onboard uwb+imu TDOA-based localization accuracy is around 20 cm RMSE in our lab.
The error in z-axis contributes the most since we only have around 2.8 meters anchor separation in z. Also, the floor and metal ceiling in our lab bring many RF reflections. With a large separation in z and more computations, the localization performance can be improved. With DW1000 UWB chips, the measurement biases also have a great impact in accuracy.
Lastly, TWR, with a proper antenna delay calibration, would have a better accuracy compared to TDOA.
Hi, How did you get the UWB measurement logged ? Thanks
Hi! You can contact the authors of this blogpost through the dynamics systems lab: https://www.dynsyslab.org/contact/